新型コロナ 株価 宅配 デリバリー 緊急事態宣言

- 点線部分は緊急事態宣言が発令された「2020-04-07」です。
- 株価のデータはAlpha Advantage社の無料APIを用いて取得しています。
- 凡例に示されている企業は2020/04/16時点で宅配事業サービスを行っております。
お笑い芸人 推定年収
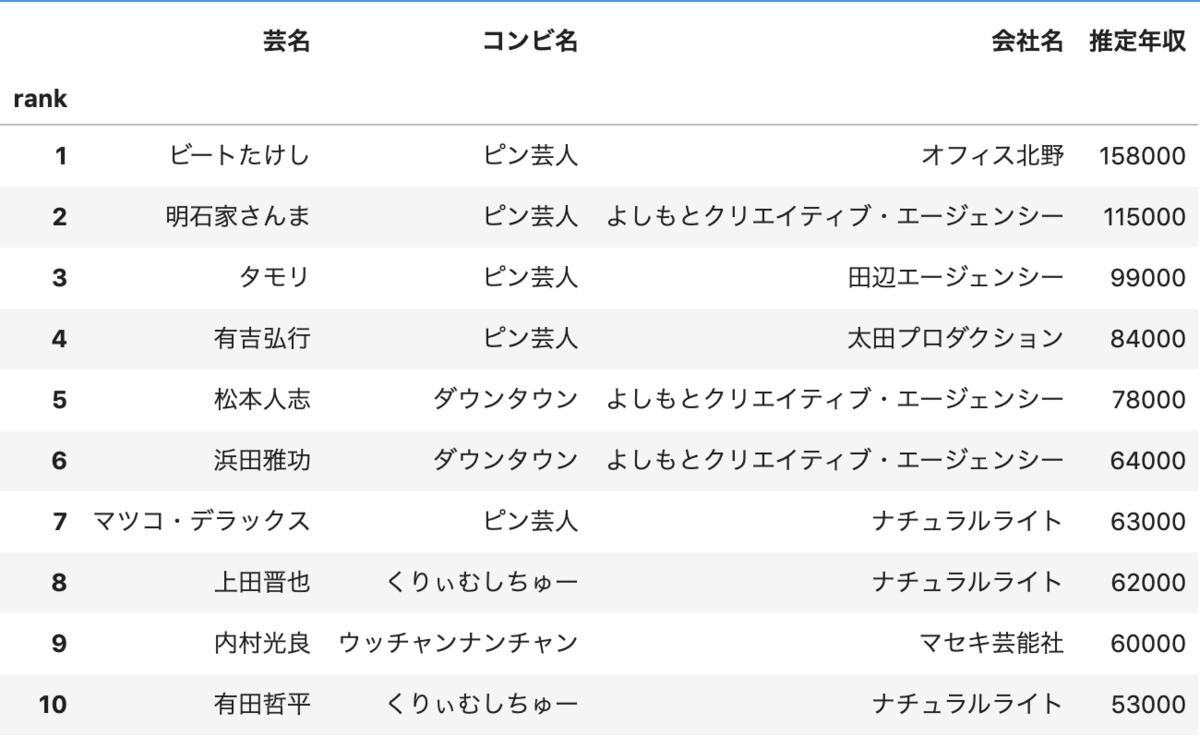


*本結果は以下のサイトを参考に作成しております。
冨乃 けい, RANK1 プロが紹介するランキングサイト, https://rank1-media.com/I0000225/ , アクセス日時 : 2019年11月19日 21:45
*免責事項
「データサイエンティストの投資成長日記」(以下、「当サイト」とします。)における免責事項は、下記の通りです。
コメントについて
次の各号に掲げる内容を含むコメントは、当サイト管理人の裁量によって承認せず、削除する事があります。
- 特定の自然人または法人を誹謗し、中傷するもの
- 極度にわいせつな内容を含むもの
- 禁制品の取引に関するものや、他者を害する行為の依頼など、法律によって禁止されている物品、行為の依頼や斡旋などに関するもの
- その他、公序良俗に反し、または管理人によって承認すべきでないと認められるもの
当サイトの情報の正確性について
当サイトのコンテンツや情報において、可能な限り正確な情報を掲載するよう努めています。しかし、誤情報が入り込んだり、情報が古くなったりすることもあります。必ずしも正確性を保証するものではありません。また合法性や安全性なども保証しません。
損害等の責任について
当サイトに掲載された内容によって生じた損害等の一切の責任を負いかねますので、ご了承ください。
また当サイトからリンクやバナーなどによって他のサイトに移動された場合、移動先サイトで提供される情報、サービス等について一切の責任も負いません。
当サイトの保守、火災、停電、その他の自然災害、ウィルスや第三者の妨害等行為による不可抗力によって、当サイトによるサービスが停止したことに起因して利用者に生じた損害についても、何ら責任を負うものではありません。
当サイトを利用する場合は、自己責任で行う必要があります。
当サイトで掲載している画像の著作権や肖像権等について
当サイトで掲載している画像の著作権や肖像権等は、各権利所有者に帰属します。万が一問題がある場合は、お問い合わせよりご連絡いただけますよう宜しくお願い致します。
無断転載の禁止について
当サイトに存在する、文章や画像、動画等の著作物の情報を無断転載することを禁止します。引用の範囲を超えるものについては、法的処置を行います。転載する際には、お問い合わせよりご連絡いただけますよう宜しくお願い致します。
家事をするか、働くか、男性と女性の賃金の違い
本記事では、1975年にJournal of Human Resourceに掲載された「Potential Biased in Measuring Male-Female Discrimination」のレビューを行う。
筆者であるPolachekは、男女の賃金差異(gender wage gap)に関する研究は数多くなされてきたが、男女差別という要因を考慮した研究は未だ少ないと述べている。これまでの研究において、男女の賃金の差異は職種や生涯における労働参加の傾向が異なるというような要因によって生じるとされてきた。これらの要因の効果は教育年数・勤続年数・年齢などをコントロールすることによって明らかにされてきたが、Polachekは男女差別という要因が無視され、それらの効果にはバイアスが生じている可能性があると指摘している。
男女の賃金に差異が生じるのは男女の賃金決定に対して構造的な問題があるからである。その構造的な問題を指摘するために以下のようなモデルを設定する。まず世帯には家事という家庭内労働と通常の労働である家庭外労働が存在する。特に結婚した夫婦によって営まれる家庭においては、男女それぞれの労働力を家庭内労働、家庭外労働にいかに分配するかという問題が存在する。そこで、このような家庭における労働分配が男女の家庭外労働に分配する労働力に差異を生み、男女の労働への人的投資行動を変化させるというモデルを設定し、このモデルが有効かどうか実証する。
Potential Biases in Measuring Male-Female Discrimination
Author(s): Solomon William Polachek
Source: The Journal of Human Resources, Vol. 10, No. 2 (Spring, 1975), pp. 205-229
時間あたり賃金の差異 ~男性と女性~
スタンフォード大学の名誉教授であり、健康経済学者であるビクター・フックス氏は
1971年に「Differences in hourly earnings between men and women」を発表した。
研究の動機
アメリカの労働市場において男性は女性より多くの賃金を獲得する、ということが通説となっている。
彼によれば、この通説に対しては
1. 男性は女性より強い
2. 男性は学生として教育を受けたのち、女性より多くの人的投資を行う(ex. OJT)
3. 男性は女性より、労働市場に密接な結びつきをもつ
4. 女性は男性より、労働における非金銭的な側面に重きを置く
5. 女性は雇用主から差別を受けることが多い
などの仮説がある。
そして彼は、男性と女性の賃金の差異は公共政策において非常に重要であると述べている。
彼が重要であると考えた理由は、
1. 女性は労働力の1/3以上を占めている
2. 男性と女性の賃金の差異は白人と黒人の賃金の差異より大きい
である。
そして、この男女の賃金の差異が女性に対する差別により発生しているのであれば、アメリカの経済システムには効率性や平等性の観点から問題があるとしている。
彼は自身の研究を、「男女の賃金の差異」、「男女の労働時間の差異」、「職種の違い」、「その他労働市場における男女差」に関する数多くの研究の前説のようなものとして位置付けている。
目的
1. 男女の賃金差のサイズを特定すること。
2. また、産業・職種毎にそのサイズがどれだけ異なるかを特定すること
データ
・1960年の人口住宅調査(Census of Population and Housing)における個票データである。
このデータは、全ての産業・職種・労働者階級を網羅している点に強みがある。
・賃金のデータ
男女で年間の労働時間に差があるため年収ではなく時間当たり賃金を用いる。
・欠点
1. 収入・労働時間のデータが家計のインタビューに基づいており、第三者によってチェックされていない。
2. 週当たり労働時間は1960年の人口住宅調査のデータに基づき、週当たりの勤労所得は1959年のデータに基づいている。
しかしこれらの欠点は、前著やその他の研究から考えると、
本サンプルの有用性を低下させず、本研究の目的達成の障害にはならないと言及している。
データ処理
1. 非農業従事者を以下のカテゴリーで分類
1. 性別
2. 人種
3. 年齢
4. 教育年数
5. 都市サイズ
6. 労働者階級
7. 結婚ステータス
8. 通勤時間
2. 上記のカテゴリーからより詳細なグループを1万超生成。
ex. "男性"かつ"白人"かつ"20代"かつ...
1. 5万超のサンプルサイズをグループに分類
2. 少なくとも1人を含むグループは約4500
3. 各グループ内の年収合計、労働時間合計を計算。
4. 各グループ内の時間あたり賃金を導出
5. 観測値が50以下のグループは除外 or フラグをたて明示
3. 男女の賃金差は、男性の賃金に対して女性の賃金は何%かという方法で示した。
4. グループ間の差異は、単回帰、重回帰にダミー変数を組み込むことで明示した。
結果
男女の賃金差異
1. サンプルにおける女性の賃金は男性の賃金の60%であった。
2. サンプルにおける結婚している女性の賃金は結婚している男性の賃金の58%であるのに対し、一度も結婚していない女性の賃金は一度も結婚していない男性の賃金の88%であった。この現象の背景には、結婚している女性は結婚していない男性と比較して、労働を行うインセンティブが少ないこと(収入を男性に依存している可能性がある)などがあると考えられる。
男女の賃金差異に対する女性差別仮説
男女の賃金差異に対する女性差別仮説とは、男性と女性の間の賃金の差異を発生させているのは職場における女性差別である、という仮説のことである。もしこの仮説が正しいのであれば、職場環境を自分でコントロールできる自営業者である男性と女性の間には賃金差が存在せず、職場環境を自分でコントロールできない民間企業に勤める男性と女性の間には賃金差が存在することになる。データによれば、
1. 自営業者である女性の賃金は自営業者である男性の賃金の41%であり、民間企業に勤める女性の賃金は民間企業に勤める男性の賃金の58%
であった。つまり民間企業と比較して自営業者の方が男女の賃金差があるため、前述の仮説は棄却される。なお、自営業者の男女に賃金差異が生じているのは、顧客による性別差別が考えられる。例えば自動車修理の個人商店で男性が運営している商店と女性が運営している商店であれば、顧客は男性が運営している商店に自動車修理を依頼したいかもしれない。
年齢と結婚ステータス
結婚しており配偶者がいる男女の賃金差異は年齢とともに増加していく。20代前半の結婚している女性の賃金は結婚している男性の賃金の約80%であるが、50代後半では約60%となる。一方で、結婚していない男女の賃金差異は年齢の増加とともに変化せず、女性の賃金は男性の賃金の約80~85%で一定である。
根性をモデル化する体系的なアプローチ その1
本エントリーから、
「A Systems-Approach Model of Mental Toughness:Understanding Inputs, Processes and Outputs」
のレビューを行なっていく。
Abstract:
本研究では、根性を「インプット」、「プロセス」、「アウトプット」からなる体系的なシステムのもとで理解していく。例えば、
・母親に「テストよく頑張ったね、また頑張るんだよ」と「インプット」を受けた子どもが、
・自宅で精力的に勉強をするという「プロセス」を通じて、
・再びテストで高得点という「アウトプット」を出す
というシステムは世界中の家庭で存在しているであろう。誰しも子どもの頃、テストで結果を出すためには、友達と公園で遊ぶ時間を短くして、根性を出して勉強をしなければならないことを理解していたはずである。このような子どもの根性、精神的タフさをシステム化し理解することは、子どもの才能を伸ばし、子どもの成長を円滑にサポートすることにつながるかもしれない。この子どもの根性に関する話はあくまで例であるが、根性を理解することは何らかの成果を生み出すだろうと容易に想像される。
根性に関しては数多くの研究がなされているが(Hardy et al 2014)、根性の「インプット」、「プロセス」、「アウトプット」というシステムに関しては未だ研究されていない。
参考文献
Sarah Sorensen, Grant Schofield, Aaron Jarden(2016) "
A Systems-Approach Model of Mental Toughness:Understanding Inputs, Processes and Outputs", Psychology ,Vol.7 No.12 , November 2016
~操作変数法~ 20180927
操作変数法のモチベーション
① OLS推定はバイアス、不一致の可能性がある
② 代理変数が見つからない可能性がある
① 欠落変数が時間を通じて変化する可能性がある
OLS推定は説明変数と誤差項に含まれる要因が相関すると、不偏性、一致性を満たさない。
解決方法として、まず代理変数を説明変数としてモデルに加える方法がある。例えば、賃金方程式において、誤差項には観測することのできないabilityが含まれているが、IQスコアでそれを代替することができる。
係数推定量が望ましい性質を持つための別の方法として、パネルデータを得、固定効果推定を行う方法がある。この方法により、欠落変数が時間を通じて一定である場合、その影響を取り除くことができる。
ただし、②、③が常に利用できるとは限らない。利用できない場合、別の方法を考えなければならない。その一つが操作変数法である。
操作変数法
操作変数とは、
①
かつ
②
を満たすzのことである。
①の仮定をinstument exogeneity
②の仮定をinstument relevance
という。①によって、これまでの説明変数は内生変数と外生変数
に区別できる。